ニュース


迷光解析について(その3)
迷光を正しくかつ効率的にモデル化するには、利用可能な散乱モデルから最適なものを選択し、十分な量の散乱光が目標領域に到達するようにシステムをセットアップする必要があります。
散乱モデルとインポータンスサンプリング(重要度サンプリング)オプションというFREDの優れた選択肢は、正しいシミュレーション結果を迅速に得るために不可欠です。この記事では、簡単なケースと、より複雑な多重散乱モデルをご紹介します。

図1. 同一面に散乱効率の異なる散乱モデルを設定することができます
代表的な表面散乱
FREDの表面散乱モデルは通常、パラメータ形式(数学的モデル形式)、表形式(測定データおよびオプションでカタログなどからフィッティングしたデータ)、スクリプトを用いて独自の散乱関数を自由に作成、という3つのカテゴリーに分類されます。
| Type | Model | Description |
|---|---|---|
| Tabulated 表形式 | Tabular BSDF (表形式BSDF) | 補間したBSDF分散データ |
| Tabulated PSD (表形式PSD) | 表面プロファイルデータから補間したBSDF分散データ | |
| Diffuse Polynomial(拡散多項式) | フィッティングされた測定値の表形式データ | |
| Diffuse Binomial(拡散多項式) | フィッティングされた測定値の表形式データ(ただし、平面対称分布) | |
| Parameterized パラメータ形式 | Lambertian (完全拡散) | 理想的な散乱である完全拡散 |
| Harvey-Shack(バービーシャック) | 研磨面の微細な凹凸による散乱 | |
| Extended Harvey-Shack(拡張ハービーシャック) | ハービーシャックに角度依存性を加えた散乱 | |
| ABg | A、B、gのパラメータを用いて表現する研磨面の微細な凹凸による散乱 | |
| Flat Black Paint (平面黒色塗装) | Aeroglaze Z306(オーストラリアCallington社製塗料)に基づく散乱 | |
| Surface Particle (Mie) (表面粒子 ミー散乱) | 表面の微粒子による散乱 | |
| K-Correlation(K-コリレーション) | PSD形式のマイクロラフ散乱 | |
| Phong(フォンの反射モデル) | BRDF=COS nθの関係式に従った散乱 | |
| Scripted スクリプト形式 | スクリプト | BASICスクリプトを使用したユーザ定義 |
| 拡張スクリプト | 偏光に対応した、上記スクリプト |
これらの散乱モデルは、反射または透過で適用するように選択でき、更にオプションで鏡面反射光線を除去して正しい拡散表面とすることができます。
散乱の効率的なモデリング
レイトレーシング場面では、面から散乱の定義によって計算されたパワーを持ついくつかのランダムな光線を生成することによって、散乱計算を実行します。
ここでは、高反射率の完全拡散反射面の簡単な例を見てみましょう。
完全拡散面の上方には、散乱後の光線が入射する、別の光学系として有効径を持った明るさ絞りを表わす環状領域を配置します。簡単のために、この絞りの後ろに検出器を置き、環状絞りに入る散乱光線の数を測定したいと思います。

図2. インポータンスサンプリングがない場合の、半球方向に拡散散乱放射される高反射率の完全拡散面。全散乱光線の0.8%のみが絞りを通過して検出器に到達する。
光線をあらゆる方向にランダムに発生させることが必要な場合もありますが、上記のようなモデルでは、特定の方向(環状明るさ絞り方向)に散乱した光線のパワーを測定することが目的であるため、これは非常に非効率的な方法です。生成された1000本の散乱光線のうち、必要な目標領域に到達したのはわずか8本です。
「インポータンスサンプリング(重要度サンプリング)」を使用することで、特定の方向に向かう光線のみを生成することでこの問題を解決し、検出器でより多くの信号を導くことができます。
FRED は6種類のインポータンスサンプリングに対応しています。
| タイプ | 概要 |
|---|---|
| 光線を任意の方向に散乱 | 円錐体の回転軸の角度方向を指定したユーザ定義の散乱 |
| 鏡面反射方向に光線を散乱 | 鏡面反射光を中心軸としたユーザ定義の円錐体方向に散乱。 |
| 物体に向けて光線を散乱 | 箱構造の境界としての物体方向に向かって散乱。箱構造は回転対称形状でなくても可能。 |
| 点の方向に向かって光線を散乱 | 空間の特定ポイントを中心としたユーザ定義による円錐体の回転軸の持つ角度方向への散乱 |
| 楕円体に向けて光線を散乱 | 特定の点を中心とした楕円体に向かって散乱(非回転対称も可能) |
| 閉曲線を通る光線による散乱 | ユーザ定義による閉曲線への散乱(非回転対称も可能) |
光線が目標領域に向かって散乱するようにする為には、環状の絞り内に球状のターゲットを置き、この方向に光線を導く方法があります。FREDでは、点または楕円体に散乱するオプションのいずれかを使用して、これを実現することができます。

図3. インポータンスサンプリングの対象を表す球体(楕円)の拡大図、球体は検出器前方の環状絞りの中心にセットします。
FREDに於けるこのセットアップの定義方法を図4と図5に示します。

図4. 拡散特性とインポータンスサンプリング(目標領域の方位)。同時に複数の散乱モデルと目標領域を定義し、アクティブにすることができることにご注目ください。

図5. 球状ターゲットの定義です。 各インポータンスサンプリングタイプには、散乱光線の数や散乱系統の数をカットオフとして制御するオプションがさらに用意されています。
この定義は半球方向に散乱するすべての光線を扱う一般的な方法よりもはるかに効率的です。

図6. 球体への散乱は、インポータンスサンプリングを行わない場合よりも効率的ですが、散乱面から見ると円形の環状絞りが楕円に見えるため、まだ理想的とは言えません。
しかしながら、それでも、生成された1000本の散乱光線のうち、環状絞りの目標領域まで到達したのは462本でした。これは、インポータンスサンプリングを行わなかった場合の0.8%の効率からは大きく向上していますが、この結果は、環状絞りに対して角度の大きい入射光について平面絞りと球体ターゲットを使用することの限界も示しています。 実際には、下記の光学系の明るさ絞りを表す環状は、散乱面から見ると楕円形につぶれており、これは球形状では十分に表現することはできません。 この場合、FREDが提供する他のインポータンスサンプリングオプションのうち、おそらく最もシンプルで効率的なアプローチは、曲線が環状表面の開口部を記述する「Scatter rays through a closed curve」(閉曲線を通る光線による散乱)を使用することです。

図7. 環状に配置された(円形の)カーブへの散乱。この場合、100%の光線が環状部を通って検出器に到達します。
| インポータンスサンプリングの使用 | 効率性 |
|---|---|
| 無し | ~0.8% |
| 球体への散乱 | ~46% |
| 曲線への散乱 | 100% |
以上のように、インポータンスサンプリングと光線の効率性の結果を比較すると、どの手法を選択するのかということの重要性が分かります。
複数のターゲットに対する複数の散乱のモデル化
上記の例では、1つの散乱モデルと1つのインポータンスサンプリングとを組み合わせて使用しています。これは単純な状況では問題ありませんが更にFREDは同じ表面で複数の散乱モデルとターゲッ,トを配置することが可能です:
- 反射散乱関数と透過散乱関数が異なる面
- マイクロラフネス(Harvey-Shack)と微粒子汚染(Mie)の両方を示す研磨面のように、異なる散乱特性を示す表面。
- 複数の方向に優先的に散乱する表面
最後の例は、第一散乱面からの光を再散乱させる第二散乱面を追加する事例となります。さらに複雑にするために、第二散乱面は傾いた六角形の平面とします。これは球ではうまく表現できない形状です。下記の光線追跡結果はその効果を示しています。

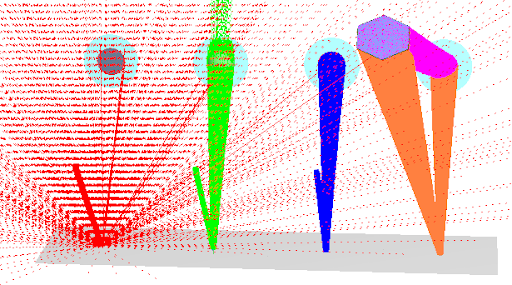
図8. 傾いた六角形の平面からの二次散乱の例。二次散乱光線は赤紫色で示しています。
このシミュレーションでは、第一散乱面には、表面拡散と粒子散乱の両方を表現する2つのアクティブ散乱モデルと、2つの目標方向(1つは環状面、もう1つは六角形表面)を持っています。第二の散乱面は、環状帯に向かって散乱するように設定されています。

図9. 一次散乱面への複数の散乱モデル・散乱方向の適用
FREDの散乱のユーザインターフェースでは、定義を失うことなく、必要に応じてモデルのオフ/オンに切り替える機能もあることにご注目ください。
まとめ
FREDは13種類の散乱モデルと6種類のインポータンスサンプリングを保持しており、迷光解析のような難しい散乱問題を簡単にシミュレーションするための幅広い選択肢を提供します。FREDのインポータンスサンプリングオプションは、必要な光線の数を減らし、計算時間を短縮する、非常に効率的な光線追跡を可能にします。
